贝叶斯公式
贝叶斯公式·概率论
其中
如果让
不难理解。
移项得贝叶斯公式。
题外话:条件概率谬论
条件概率谬论认为,
考虑一个现实的情景:检测一种疾病,对于阳性个体有
约定
明确题目所求:
由贝叶斯公式得
需求
分讨。
- 如果该人为阳性,且正确检出,概率
- 如果该人为阴性,且错误检出,概率
综上有
则
即如果被检出阳性,则真正患病的概率为
更加深度地讨论这个问题,
我们不妨认为阳性误检率和阴性误检率相等即
那么
所以
这个函数在
分析此函数图像(
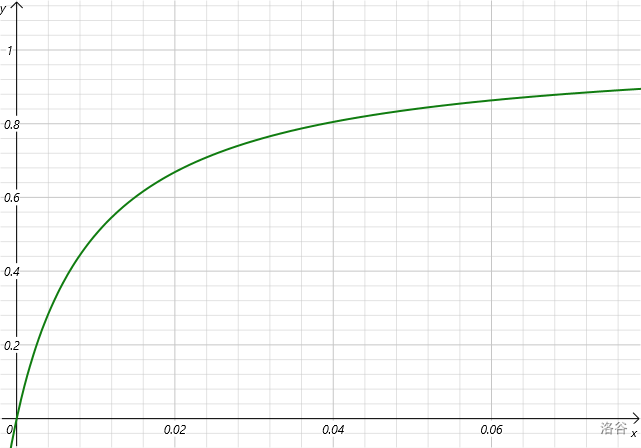
我们发现在